Normal distributions and \\(\pi\\)

Normal distributions are a class of continuous probability distribution for random variables. They often show up in measurements of physical quantities. For example, the human height is normally distributed. In fact, it is claimed that variables in natural and social sciences are normally or approximately normally distributed. Weight, reading ability, test scores, blood pressure, \(\ldots\)

The underlying reason for this is partly due to the central limit theorem. The theorem says that the average of many observations of a random variable with finite average and variance is also a random variable whose distribution converges to a normal distribution as the number of observations increases. This conclusion has a very important implication for Monte Carlo methods which I will discuss in another post.

In the simplest case (zero mean and unit variance), the distribution is written as \begin{equation} f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}. \nonumber \end{equation} If we plot the function \(f(x)\), the curve looks like the following

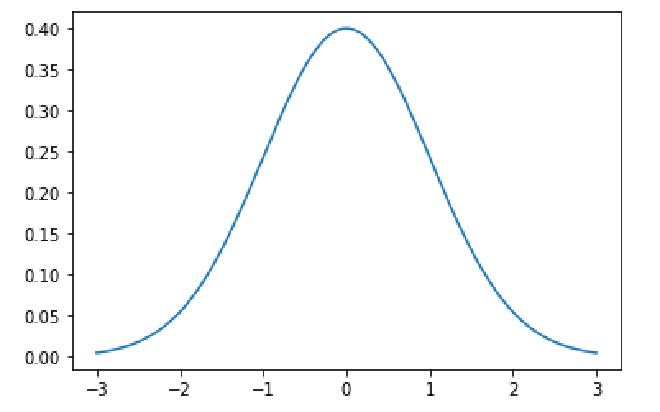
The prefactor \(1/\sqrt{2\pi}\) of \(f(x)\) is its normalization constant which guarantees that the integration of \(f(x)\) over the entire real axis is unity \begin{equation} \int_{-\infty}^\infty f(x)dx = 1. \nonumber \end{equation} We all know that the mathematical constant \(\pi\) is the ratio of a circle’s circumference to its diameter. This brings up an interesting question: why does \(\pi\) show up in probability distributions that seemingly have nothing to do with circles?

The reason, it turns out, boils down to how the normalization of a normal distribution is calculated. A normal distribution belongs to a type of function called the Gaussian function \(g(x) = e^{-x^2}\). Its integral is \begin{equation} \int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi}.\nonumber \end{equation}

Standard approach

#

A textbook approach for getting the normalization constant is to compute the square of the Gaussian integral \begin{equation} \left(\int_{-\infty}^\infty e^{-x^2}dx\right)^2 = \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-(x^2+y^2)}dxdy. \nonumber \end{equation} In this way, we can leverage the coordinate transformation to map the Cartesian coordinates \((x,y)\) into polar coordinates \((r,\theta)\) using the identity \begin{equation} x^2+y^2 = r^2, \nonumber \end{equation} which is exactly an equation of a circle with radius \(r\). It is through this equation (transformation) that allows \(\pi\) to have a place in the normal distribution. To continue, the square of the Gaussian integral now becomes

\begin{align} \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-(x^2+y^2)}dxdy &= \int_0^{2\pi}\int_0^\infty e^{-r^2} \,r drd\theta \nonumber \\\ &= 2\pi\int_0^\infty \frac{1}{2} e^{-y} dy,\,\,\,\,\,\,\text{where}\,\,\, y=r^2 \nonumber\\\ &= \pi. \nonumber \end{align}

As a result, the normalization of the Gaussian function is \(\sqrt{\pi}\).

Contour integration

#

Of course, the method described above is not the only way to normalize the Gaussian integral. There are many proofs ranging from differentiation of an integral, volume integration, \(\Gamma\)-function, asymptotic approximation, Stirling’s formula, Laplace’s original proof, and the residue theorem.

Speaking about the residue theorem, it is a powerful tool for evaluating integrals. The theorem generalizes the Cauchy’s theorem and says that the integral of an analytic function \(f(z)\) around a closed contour \(C\) depends only on the properties of a few special points (singularities, or poles) inside the contour.

\begin{equation} \int_C f(z) dz = 2\pi i\sum_{j=1}^n R_j, \nonumber \end{equation}

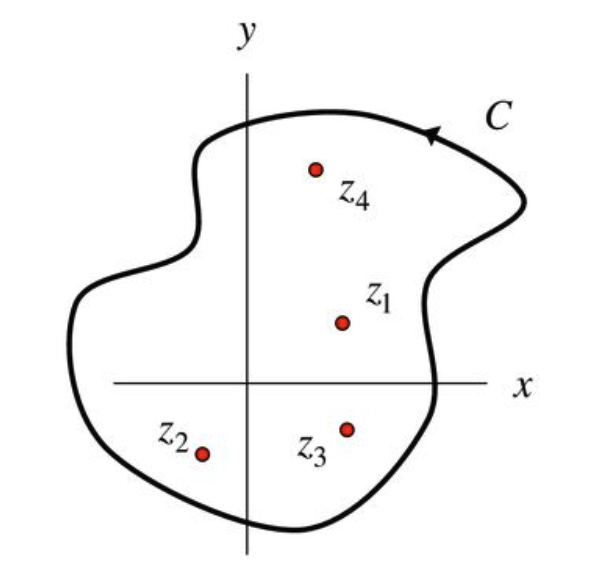
where \(R_j\), one of those special points, is called the residue at the point \(z_j\):

\begin{equation} R_j = \frac{1}{2\pi i}\oint_{C_j} f(z) dz. \nonumber \end{equation}

So the residue theorem by definition has a prefactor that contains \(\pi\). However, if we want to apply the theorem to the Gaussian function, we would hit a wall. This is because the complex Gaussian function \(g(z) = e^{-z^2}\) has no singularities on the entire complex plane. This property has bothered many and in 1914 a mathematician G. N. Watson said in his textbook Complex Integration and Cauchy’s Theorem that

Cauchy’s theorem cannot be employed to evaluate all definite integrals; thus \(\displaystyle\int_0^\infty e^{-x^2}dx\) has not been evaluated except by other methods.

Finally in 1940s, several proofs were published using the residue theorem. However there proofs are based on awkward contours and analytic functions that seem to come out of nowhere. For example, Kneser has used the following definition ¹ $$ \frac{e^{-z^2/2}}{1-e^{-\sqrt{\pi}(1+i)z}}. $$ Basically the idea is to construct an analytic function that looks like the Gaussian but with poles so that the residue theorem can be applied.

While I like the beauty and power of the residue theorem, the complex analysis proof just seems too complex and artificial for my taste. The standard textbook proof is simple and incorporates naturally the reason why $\pi$ is there in the normalization. Anyway, I found this little fact a bit interesting.